1.はじめに―論理的に考える―

論理的に考えて，その筋道を素直に書いていけば，論理的な文章ができます．
論理的に考えるには，そのように考えられる道具（ツール）を使います．

ここでいうツールとは何もトンカチや定規ではありません．
論理的に考えることのできる言葉と方法です．
これを論理ツールと言いましょう．

論理ツールは2種類あります．

一つ（論理ツール①とします）は，言葉の示す範囲を決める基本的な言葉です．
基本論理語といいましょう．論理を作るのは言葉です．
言葉の示す範囲が決まれば，考える範囲が決まりますから，考えることが容易になります．

もう一つ（論理ツール②とします）は，考える方法で，その方法のとおりに考えると，
私たちはそれを筋道の通った考え方と言います．
論理的な思考法です．

論理ツール①も②も人類が進化の過程で獲得したもので，このツールを使って考えると，
私たちは納得でき，課題に対して適切な解決法を見いだすことができます．

だから人類は生き延びたのだし，文明を生み出したのです．

逆に言えば，そのような考え方を身に付けて文明を誕生させたから，
それを筋道の通った正当な考え方とし，「論理的」と言ったのです．

2．論理ツール①（基本論理語）

論理ツール①は，あなたの使う言葉の示す範囲を決める基本的な言葉（基本論理語）です．

この言葉をうまく使いこなすと，あなたの考える対象が明確になり，考える範囲が決まります．
余計なことまで考えなくてよくなるのですから，考えることが容易になります．

基本論議語は以下の6種類です．

順番に説明します．

1）包摂と同一

「AはBである」という命題で説明します．
命題という聞き慣れない言葉が出てきました．

命題とは，主語と述語のそろった文で，意味を考えることができる文です．
その書かれていることが正しいのなら，真といい，間違いなら偽といいます．

この命題のAとBの関係を考えます．

A（主語）とB（述語） の関係は2つあります．
命題に2つの意味があると言ってもよいです．

1つは包摂（含まれる）で，
もう一つは同一（同じ）です．

それらを図示します．

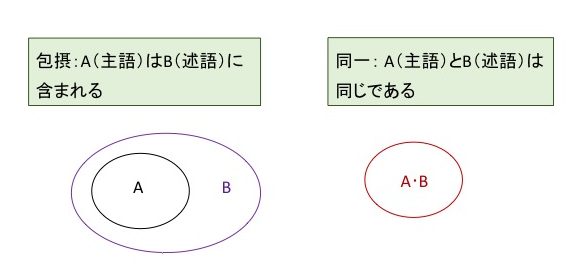
包摂は，AがBに含まれることです．
図に示すようにBの中にAのすべてが含まれます．

たとえば，「犬は動物である」は，犬（A）は動物（B）に含まれます．
犬は動物の一種で，犬以外にも猫や馬など動物は他にもいます．
主語（A）が示す概念に対して，述語（B）が広い概念を持つことは，この図からもわかります．

もう一つの同一は，AとBが同じであるものです．
図に示すように，AとBの範囲はピッタリと合っています．

たとえば「犬はドッグである」や「Hは水素原子あるいは水素元素を示す元素記号である」です．
主語で示されることと，述語のそれと同じであり，それ以外のことを含みません．

「犬はドッグである」という文は，「犬は犬である」ということです．
これは同じことを言っているのです（トートロジーと言います）．

「Hは水素原子あるいは水素元素を示す元素記号である」は「H」という元素記号の定義文です．
確かに，Hという元素記号は水素原子や水素元素のみを示して，それ以外は示しません．

「He」だと「Heはヘリウム原子あるいはヘリウム元素を示す元素記号である」です．

以上述べた命題はいずれも真（正しい）です．

2）「すべて」，「ある」と「ほとんど（ほぼ）」

「すべて」，「ある」，「ほとんど」を説明します．

「ほとんど」は「ほぼ」と言い換えてもよいです．
これは命題「AはBである」のAがどの程度Bに含まれるかを示します．
AとBの関係は3種類あります．

それらを図に示します．
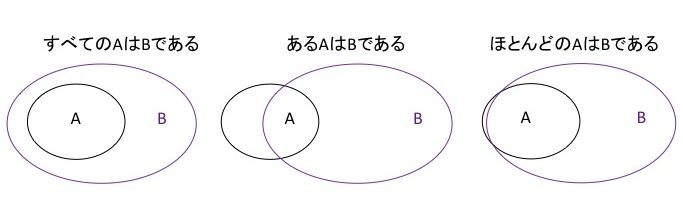※正確には主語は「Aは」で述語は「Bである」ですが，ここでは主語をAとし述語をBとして進めます．

第一は，「すべてのA はBに含まれる」です．これは包摂のことです．

たとえば，「すべての犬は動物である」です．
世界中のどこの犬でも，すべての犬は動物です．
この命題は真です．

第二は，「一部のAはBに含まれる」です．
「一部」を「ある」とします．

例をあげます．
「ある犬は動物である」はこの命題です．
これは偽です．動物でない犬はいませんから．

第三は，「ほとんどのAはBである」です．
「ほとんど」は「ほぼ」と言ってもよいです．

たとえば「ほとんどの犬は動物である」です．
この命題は，少なくとも一匹の犬は動物ではないことを示します．
これはありえませんから，この命題は偽です．

3）「すべて」，「ある」，「ほとんど」の数学的表現

「すべて」，「ある」，「ほとんど（ほぼ）」を，数学的に表現すると，
科学技術者には馴染み深くなります．

「すべて」は文字どおり100％です．
これは「＝」と書けます．

たとえば，「すべての鳩は鳥である」です．
これは「100%の鳩は鳥である」と言い換えられます．

世界中のすべての鳩は鳥ですから，この命題は真です．

「ほとんど」は何%でしょうか．
科学技術で馴染み深い標準偏差で考えるとわかりやすいです．

「ほとんど」は標準偏差の2σと考えると納得できます．
2σは95％ですので，「ほとんど」は「95%以上100%未満」となります．

AがBに含まれる割合をXとしますと，「ほとんど」は「95%≦X＜100%」となります．

そうなると，「ある」は「95%未満（X＜95%）」になります．

「ほとんど」は「≒」とも書けます．これは科学技術では近似解として使われます．

4）同一は難しい

前項で、ほとんどを「≒」と記しました．
「同一」である「＝」と「ほとんど」である「≒」は本来異なるものです．

しかし，科学技術ではこの区別は哲学や数学より少しゆるいです．
科学技術者が≒を使うとき注意が必要です．

哲学者ライプニッツは，「同一であること」を
「Aのもつすべての性質をBが持ち，同時にBがもつすべての性質をAが持つとき」と言いました．

図示します。

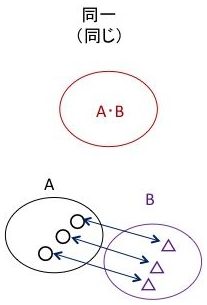
図に示すように、ライプニッツの考え方だと，
Aの各要素とBの各要素には，厳密に1：1の対応関係が成り立ちます．

数学の「＝」も「同一」です．

たとえば，「2＝1＋1」です．
この考え方だと，Aの要素とBの要素を入れ替えても同一は成立します．

1＋1＝2も2＝1＋1も左辺と右辺を入れ替えても成立します．
科学技術者は，「同一」の概念をもう少し広くとらえています。

科学技術では「≒」は近似解で，「ほとんど同じ」ととらえています．
科学技術者は近似解に慣れています．

確かに現実の科学技術では正確な値が求められないことが多いから，
近似解で物事を進めるケースが多いです．

このように近似解に慣れているので，
科学技術者は，「＝」と「≒」を同一視することがあります．
そうしないと研究開発が進まないことがあるからです．

しかし，「＝」は「同一」で「≒」は「近似解」ですから，
これらは本来区別すべきもので，同一に取り扱うことができないものです．

そのことが思わぬ間違いや事象の拡大解釈や恣意的解釈につながる危険性があります．

科学技術者は，もっと厳密に「＝」と「≒」の違いを理解し，これらを区別して使うべきです．

5）「かつ」と「または」

「かつ」か「または」により命題の対象とする範囲が変わります．

「AかつBである」は，Aでありそれと同時にBでもあることです．
図のAとBの重なっている領域です．

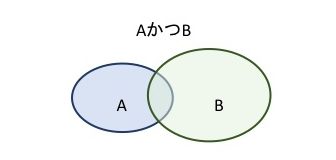
たとえば，「イケメンでかつ背の高い人」は「イケメン」でありそれと同時に「背が高い」ことです．
この2つを同時に満たす人は多くはないですね．

現代物理学で電子の振る舞いは，「粒子でありかつ波動である」と書かれます．
これは，電子は「粒子」でありそれと同時に「波動」であることを示します．

一般常識からはかけ離れた概念ですが，
現代物理学が教えてくれるミクロの粒子（素粒子）の振る舞いです．

「AまたはBである」は，Aの領域かBの領域であることを示しますから，
対象はAとBの全領域になります．

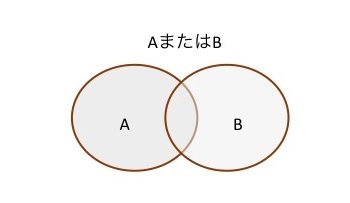
たとえば，「イケメンまたは背が高い人」は「イケメン」か「背が高い」かのどちらかです．
上の「かつ」よりはバリヤーが低いですね．

「粒子であるかまたは波動であるもの」を考えてみましょう．

これは，「粒子」か「波動」かどちらかです．
粒子でも波動でもよいのですから，身のまわりにある石やボールは粒子ですし，
池に石を投げ入れて時の波や海岸のうねりも波です．

これらすべてが対象になります．随分と範囲が広がりました．

6）「～でない（命題）」（否定）

論理的に考えるとき，否定は大事です．
決してネガティブで後ろ向きの思考ではありません．

命題の真偽を判定する方法ですし，新しいことを考え付く原動力です．

命題「Xである」に対して，「Xでない」が否定です．
これを否定命題といい，X(―)で表しましょう．
図のX以外の領域です．

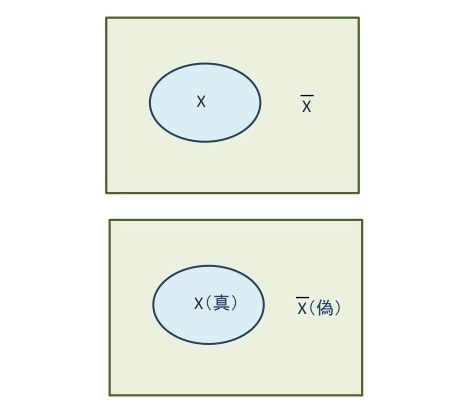
「Xである」が真なら「Xでない」は偽です．

たとえば，「犬は動物である」（X）は真です．
「犬は動物でない」（X(―)）は偽です．

一方，「Xである（X）」が偽なら「Xでない」（X(―)）は真です．
「犬は植物である」（X）は偽ですから「犬は植物でない」は真です．

否定の効能は2つあります．

1つは命題の真偽がよくわからないとき，否定命題を考えてその真偽を検討します．
否定命題が真なら命題は偽ですし，否定命題が偽なら命題は真です．
否定命題の方が考えやすいことがあるのです．

もう1つは新しい発想や考えを生み出すことです．
否定は現状や当たり前と思うことを打ち消すのですから，
そこから新しい発想や考えが生まれるのです．

否定は後ろ向きの考え方ではありません．
対象を真剣にかつ真逆に考えて，新発想を導く思考法です．

これらの否定の神髄は基本論理語の「対偶(たいぐう)」や，論理ツール②の「背理法」で発揮されます．

7）命題の逆，裏，対偶(たいぐう)

ある命題「AがBである」に対して，言葉を入れ替えます．
そうするといくつかの命題を作れます．

それらに名前が付いていて，「逆」「裏」「対偶」といい，
それぞれ真と偽を考えることができます．

命題「AはBである」と例「犬は動物である」を，もう一度取り上げます．

考えている対象を「すべて」として，以下の命題には「すべて」を付けます．

命題を示します．

逆

AとBを入れ替えると，次の命題となります．

これは命題αのA（犬）とB（動物）を入れ替えたものです．

さて，この命題は真でしょうか．必ずしも真とは言えません．

犬は動物ですが，犬以外の動物は，猫や馬など多くいます．
一部は正しい（真）ですが，間違い（偽）も含まれます．

つまり，命題αが真であっても，逆は必ずしも真ではないのです．

裏

　ちょっと馴染みのない言葉ですね．

日本語としては，「AでないものはBでない」「すべての犬でないものは動物でない」と
「もの」を補った文だとしっくりきますので，そのように書くとよいです．

「裏」をつくるときのコツです．書き直します．

確かに犬でなくて動物でないものは多くあります．
机もパソコンも犬でなくて，動物でもありません．
この点ではこの命題は真です．

しかし，犬でなくて動物であるものもいます（たとえば猫や馬）．
だから，この命題は必ずしも真とはいえません．

対偶(たいぐう)

もう一つ考えます．AとBを否定してそれを入れ替えます．この命題を「対偶(たいぐう)」といいます．

命題αを「逆」（β）にして，さらに「裏」（γ）にすると「対偶」になります．
「裏」を「逆」にしてもよいです．

これは「すべての動物でないものは犬でない」とも書けますので，書き直します．
これも対偶を創るときのコツです．

これは必ず真です．動物でなくて犬であるものはいません．

まとめ

さて，以上の関係を図に示します．

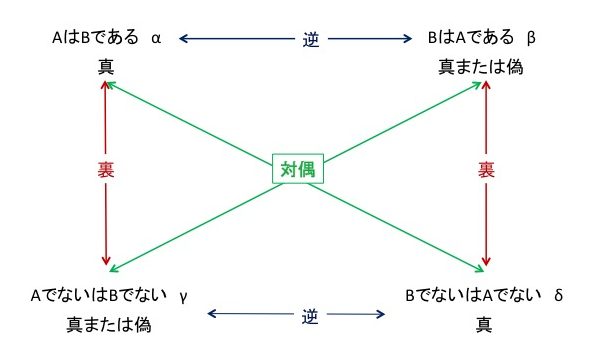
命題αが真であるとき，逆と裏は必ずしも真ではありませんが，対偶は必ず真になります．

これらの関係は命題が真か偽かを考える際に重要です．

特に，命題αの真偽がわかりにくいとき，その対偶を検討すると，
真偽の判定がしやすいことがあります．

対偶が真なら命題も真ですし，対偶が偽なら命題も偽です．