1．相関性とは

相関性とは，2つの事項AとBの間で，
一方のAが変化すれば，
それに対応してもう一方Bも変化する関係をいいます．

ある事項Aが起こり，続いて事項Bが起こったとします．
AとBの間に何らかの関係があるのかを考えたいとき，
相関性の有無を検討すると両者の関係がわかります．

2．相関性を見つける

相関性はデータを取って相関分析や回帰分析を行って判断します．

相関性を見つける簡単なプロセスを説明します．
まず相関分析を行います．ついで回帰分析を行います．

1）相関分析

①データを収集する

相関性を考察したい対象に関するデータを収集します．
ここでは予断を持たずにできるだけ多方面のデータを集めるのがコツです．

②データをまとめる

次にデータをまとめます．
収集したデータを表にまとめます．

検討しやすくするためには，
行と列の配列と項目を工夫することがポイントです．

③データを選別する

まとめたデータから最初に解析するデータを選別します．

最初に選別されたが最も意味のあるデータか否かはわかりません．

解析を進めると注目すべきデータが他にあることがみつかることが多いです．

④データを解析する

データを解析するにはグラフ化が便利です．

このとき，
x軸は要因と考えられる事項，
y軸は結果と考えられる事項とすると，
考えやすいです．

データの変化に相関性がありそうなら相関分析を行い，
xとyの相関性を調べます．

相関分析とは，xの変化に対するyの変化の度合いを調べるものです．
その結果は相関係数（r）として得られます．

相関分析はExcelソフトの関数（CORREL）を使うと便利です．

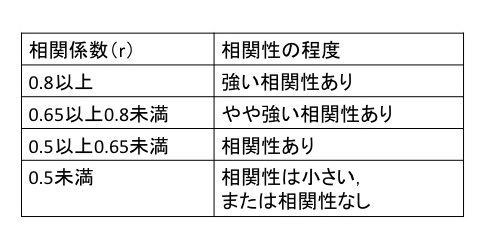
相関係数（r）から相関性を考えます．
相関係数の大きさと相関性の程度については人によってやや異なりますが，
以下の表が目安になります．

相関係数（r）が0.5以上であれば，何らかの相関性があると考えてよいでしょう．

2）回帰分析

相関性が認められれば回帰分析を行います．

回帰分析とは，グラフ上のデータ点から考えられる
最も妥当な一次近似線（回帰線）を求める方法です．
一次近似線（回帰線）と決定係数（R2）が得られます．

決定係数（R2）は，どの程度が回帰線で説明できるかを示します．

たとえば，R2＝0.5なら全体の50%がその回帰線で説明できることを示します．

R2が大きいほど回帰線がより確からしい，と言えます．

3）相関性の例

①プロ野球の成績

相関性の例として，
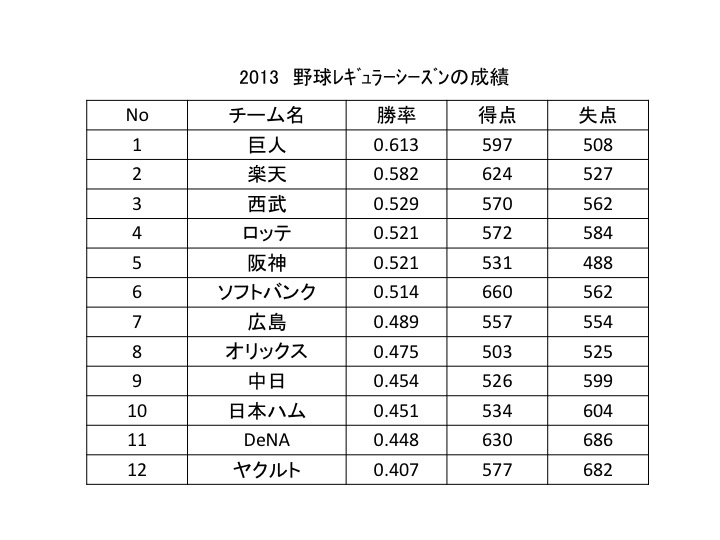
2013年プロ野球レギュラーシーズンの成績を取り上げます．

12全球団の勝率，得点および失点を，チームの勝率順に表にまとめました．

②相関分析

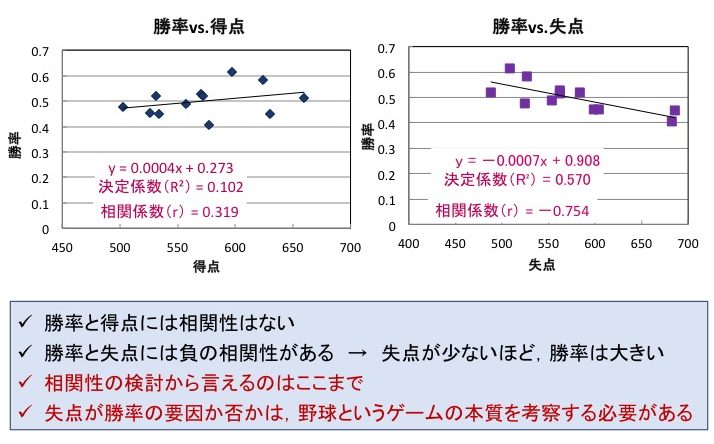
勝率に対して得点と失点のどちらが相関性を持つのかを調べました．

勝率と得点との相関係数（r）は0.319で相関性は小さいと判断されます．

それに対して，勝率と失点の関係は相関係数（r）が－0.754です．

マイナスの値になっているのは，失点が少ないほど勝率が大きくなるからです．
このケースでは相関性があるといえます．

③回帰分析

勝率と得点および失点の関係を図示します．
それぞれに対して一次回帰線を引いてみました．

勝率と得点の図（左側）では回帰線に対して
データ点は大きくばらついており，
決定係数（R2）は0.102で小さいです.
相関性が小さいことが確認できます．

一方，勝率と失点の図（右側）では
回帰線の近辺にデータ点は分布しています．
決定係数（R2）は0.570で大きく，
相関性の大きさに対応しています．

確かに，勝率と失点の間には相関性があると判断してもよいです．

では失点が勝率を決める要因なのかどうかは，
この解析からはわかりません．

別の観点や野球というゲームの本質から考察します．

④要因考察

AとBの間に相関性があれば，
多くのケースではどちらかが要因でもう一方が結果となる仮説を立ててよいです．

ただし，真の要因が見かけ上の事象に隠れているケースもありますから，
事象の本質を常に見極めるようにする努力が必要です．

上の例では勝率と失点に相関性がありましたので，
要因について仮説を立てて検討します．

仮説を「失点の少なさが勝率を高める要因である」とします．

ここで，野球というゲームについて考えてみます．

野球は自分のチームがどれだけ点をとっても，
相手チームがそれより1点でも多く点を取れば負けるゲームです．

だから，失点が少なければ勝つ確率が増えると考えるのは合理的です．

なので，失点は勝率の要因と考えられます．