1．はじめに

技術者や科学者は，何かある目的を持って実験します．
実験を行えばいくつかのデータが得られます．

データは何を示しているのか，それは目的を達成するのに貢献できるのか，考え込むことも多いでしょう．

データ量が十分で，その示すことがよくわかり，目的に対する現状の位置付けも明確である，などということはほとんどないでしょう．

多くの場合は，少ないデータで実験の方向を決めねばなりません．

実験の現況を報告するレポート（週報や月報など）では，ヤマカンや直感ではなく，論理的で合理的に実験の方向性を記述することが要求されます．

「何となく，そう思う」や「誰かに言われたから」では，上司は実験の進め方を承認しないでしょう．

少ないデータから，それの示すことを適切に推論し，推論結果に基づき進むべき方向を，わかりやすく論理的にレポートにまとめて提案できれば，あなたの提案は「わかった！提案どおりに進めてほしい．ガンバレ！」と認められ，励まされるでしょう．

本稿は，データに基づいて推論する方法と，それをわかりやすく論理的に書く方法について，述べます．

2．実験データ例

ある架空の実験データを例にとります．

1）実験内容

・試料
2つの部材からなる材料をXとします．
1つの部材をAとします．

これには類縁物質A1，A2，A3およびA4があり，それらが使われます．

もう1つの部材をPまたはQとします．

XはAPとAQ（ここで，AはA1，A2，A3またはA4）の組成です．

AをA1からA4まで変化させて，一連のAPとAQシリーズの材料が作製されます．

・物性α
この材料Xは物性αという機能を発現するとします．

APとAQの物性αは同様の挙動を示すと，いくつかのデータから示唆されているとします．

たとえば，APの物性αがA1P＜A2P＜A3P＜A4PとA1→A2→A3→A4の変化に伴い大きくなるなら，A1Q＜A2Q＜A3Q＜A4Qと，AQもA1からA4に変化するに伴い大きくなると示唆されます．

・実験の目的と現況
APとAQシリーズの材料を作製し，最も大きい物性α値を示すものを探索することが，実験の目的とします．

いま，その実験途中でいくつかのデータが出てきました．

・レポートの目的
取得したデータに基づき，最も大きい物性α値とそれを示す部材の組み合わせを推論することとします．

3．推論

1）ケース1

・実験データ
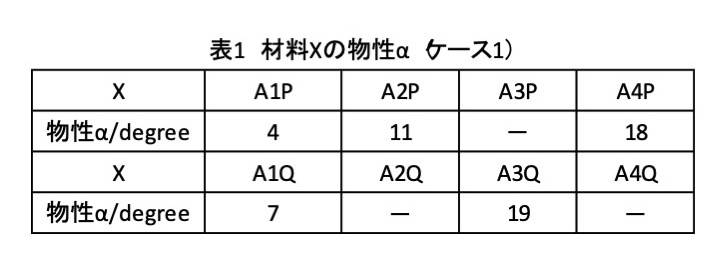
表1に示すデータが得られました．APシリーズはA3Pを除いて，物性αのデータが得られています．

AQシリーズはA1QとA3Qのみデータが得られました．

・推論
これらのデータから，最も大きい物性αを示す材料を推論します．

一般的に，2つの変数間の関係はグラフ化して，相関性を求めたり，回帰分析を行うと考察しやすいです．

解析するときの注意は，解析方法は複数ある場合が多いことに留意することです．

このケースでも2とおりの解析方法があります．
それらをすべて解析して，その後，より合理的で論理的なものを選ぶのです．

データを見たときに思い浮かぶ1つの解析方法のみを行っても，十分な解析とは言えません．ここ大事です．

このデータの解析方法は，繰り返しますが2とおりあります．

いずれもデータ数の多いAPシリーズを最初に解析して，その結果をAQシリーズに当てはめます．

その1つを説明します．データ解析の結果を図1に示します．

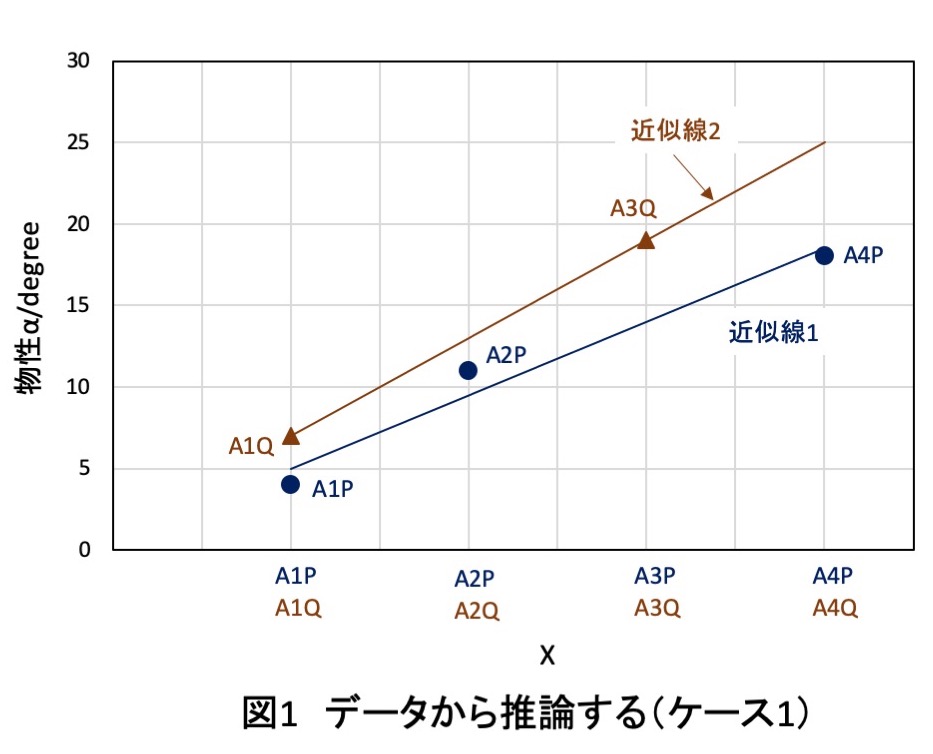
APの変化に対する物性αの変化をグラフ化します．それを回帰分析します．

ここでは回帰直線（近似直線）（一次関数での近似）（近似線1）を引いて考察します．

その結果，A1PからA4Pに変化するに伴い，物性αは直線的に増加することがわかりました．

この近似線の決定係数（R2）は0.96で十分に大きいです．

なお，決定係数（R2）は，0から1までの値をとり，1に近いほど回帰線がより確からしい，と言えます．

これまでの知見により，APの物性αの変化とAQのそれは同様の挙動を示すことが示唆されています．

だから，AQもA1QからA4Qに変化するに伴い，物性αは直線的に増加すると考えられます．

そこで，AQのデータに回帰直線（近似線2）を引きます．

AQはAPより大きい物性α値を示しますので，AQシリーズから最も大きい物性α値が得られると考えられます．

近似線2からA4Qの物性αが最も大きくなり，その値は25 degreeと推論されます．

したがって，A4Qを作製し，その物性αを測定することが提案できます．

もう1つのやり方は，回帰線を2次回帰曲線（2次近似曲線）（2次関数での近似）とするものです．

その解析結果を図2に示します．

上と同様に，APの変化に対する物性αの変化をグラフ化し回帰分析しますが，この場合は2次回帰曲線（近似線3）を引きます．

この近似曲線の決定係数（R2）は1.0で，近似線は十分に信頼できるものです．

近似線1とは異なり，A1PからA4Pに変化するに従い，物性α値は2次関数的に大きくなります．

APの物性αの変化とAQのそれは同様の挙動を示すことが示唆されていますので，AQもA1QからA4Qに変化するに伴い，物性αは2次関数的に増加すると考えられます．

そこで，AQのデータに2次回帰曲線（近似線4）を引きます．

上でも述べましたが，AQはAPより大きい物性α値を示しますので，AQシリーズから最も大きい物性α値が得られると考えられます．

近似線4からA4Qの物性αが最も大きくなり，その値は22 degreeと推論されます．

この解析方法でも，A4Qを作製することが提案できます．


さて，どちらがより確からしいでしょうか．

このケースのように決定係数が求められている場合は，決定係数の大きい方がより確からしいといえるでしょう．

だから，図2の近似線3と4が，APとAQシリーズのより確かなデータ変化だろうと推論されます．

2）ケース2

・実験データ
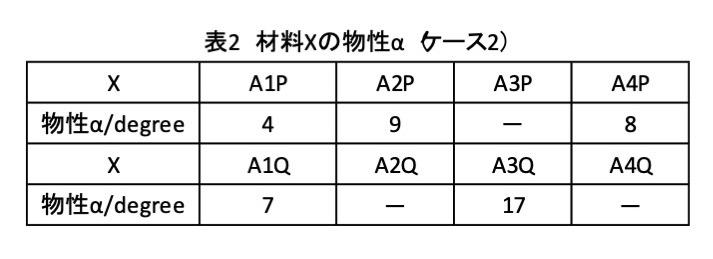
データが得られている材料はケース1と同じですが，その値が異なっているとします．
それを表2に示します．

このケースでも，どの材料が最も大きい物性αを示すのか，検討します．

・推論
このケースでも，2とおりの解析が可能です．
その1つを図3に示します．

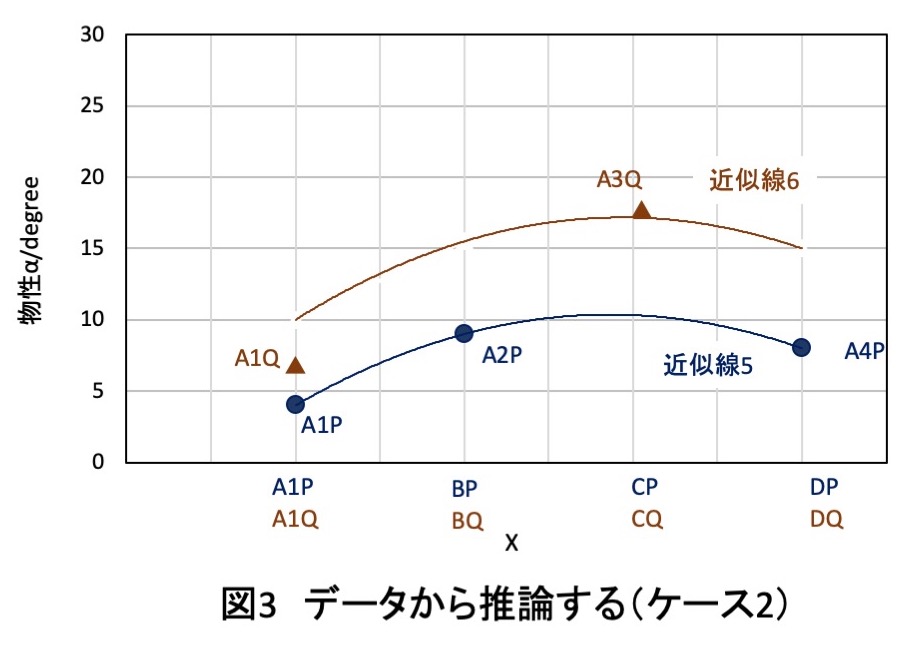
ケース1と同様に，データの多いAPシリーズを調べると，2次回帰曲線（近似線5）で近似されました．

この近似曲線の決定係数は1.0であり，近似線は確かなものと認識できます．

この近似線だとAPシリーズではA3Pが物性αの最も大きな値を与えると考えられます．

その近似線をそのままAQシリーズに当てはめると，近似線6が得られます．

A1QとA2Qのデータ点に対して近似線はいくつかの引き方がありますが，この図ではA3Qのデータと近似線を合致させました．

A3Qが最も大きい値（17 degree）を示します．

このケースでも，解析方法はもう1つあります．

それは直感に基づくもので，図4に示すような近似線を描きます．

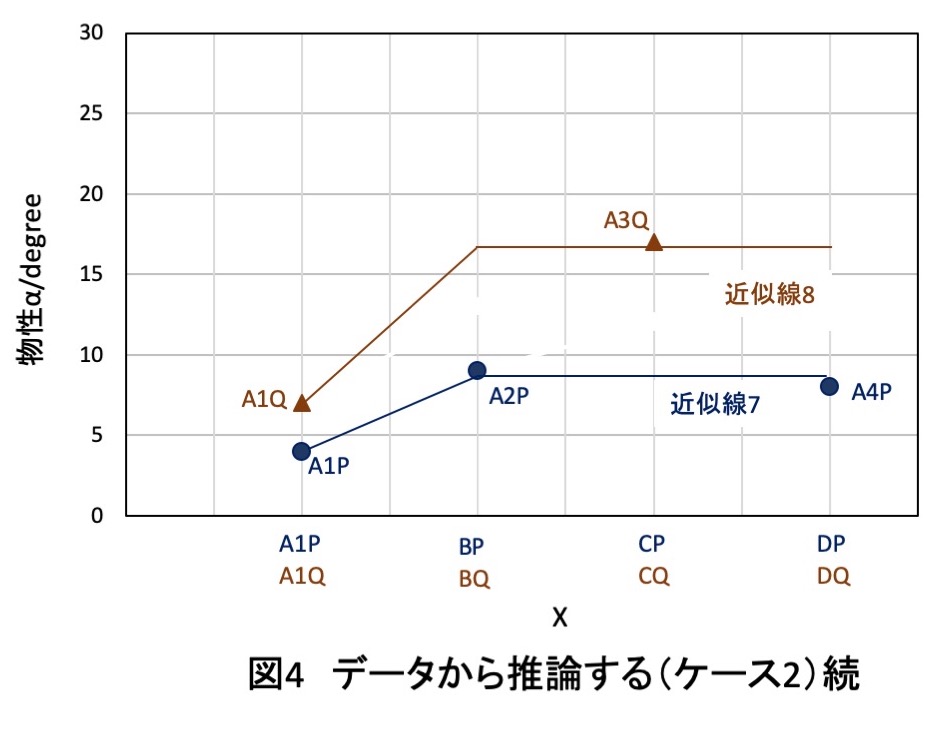
つまり，APシリーズでは，近似線7のようにA1PからA2Pまで物性αは直線的に増加しますが，A2PからA4Pではほぼ一定であり飽和している，と考えるのです．

APとAQの物性αは同様の変化をすると考えてよいから，AQシリーズのデータに同様の近似線（近似線8）を引きます．そうすると，A3Qの物性α値をとおる近似線が得られます．

この推論では，A3Qが，A2QとA4Qと同様に最も大きい物性α値（17 degree）が得られると考えられます．

これら2つの方法から同じ結論が得られ，A3Qが最も大きい物性α値を示すと考えられます．

その物性α値は実験結果によれば17degreeと明らかになっています．

目的はこれで達成されました．


さて，このケースでも2つの解析方法のうち，どちらがより確からしいでしょうか．

解析結果や決定係数では決められません．
それは，実際にA2QとA4Qを作製するとわかります．

その実験を行うか否かは，そのときの状況によりますが，作製して物性αを測定するのがよいでしょう．

どちらの推論が正しいかわかりますし，APとAQの変化の本質が何かを考察するデータにもなります．

また，何かの都合でA3Qが採用できなくなっても代替物を用意できるからです．

不都合なことは何もありません．

4．レポートの書き方

レポートの書式と書き方は，以下のとおりです．

ケース1を例にとって，レポート例を示します．

なお，ケース2は，2つの近似方法のうち，より合理的だと認識する方法を選んで，それに基づいてレポートを書くとよいです．

ケース1のレポート例

1）題名
材料Xの物性αの最高値を推論する

2）本文
・目的
2つの部材（AとPまたはQ）からなる材料X（APおよびAQシリーズ）を開発している．

材料Xは物性αを発現するが，その最高値とそれを示す部材の組み合わせはまだ見積もられていない．

そこで，これまで取得したデータから，その最高値を推論したので，以下に報告する．

・実験データ
表1に示す実験データが得られている．

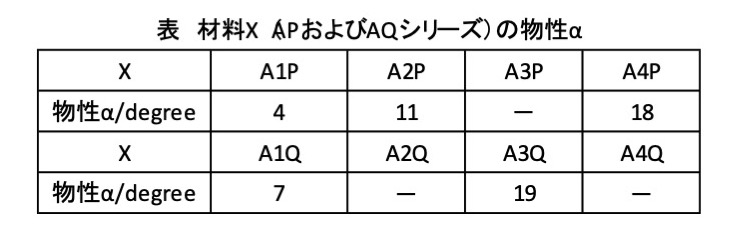
・推論
データ解析プロセスは以下のとおりである．

APシリーズのデータ数が多いので，まずAPの変化に対する物性αの変化をグラフ化し，それを回帰分析して考察した．

ついで，その結果をAQシリーズの変化に当てはめて検討し，最も大きい物性α値とそれを与える部材の組み合わせを推論した．

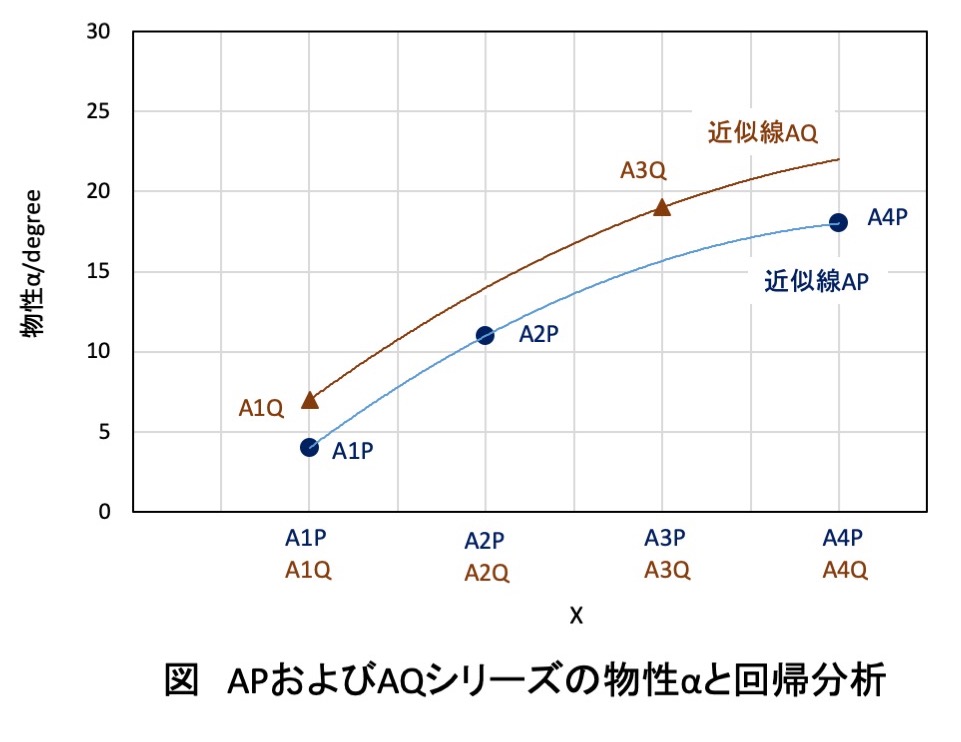
データと回帰分析の結果を図に示す．

APシリーズのデータは，2次回帰曲線（近似線AP）で近似された．

この近似曲線の決定係数（R2）は1.0で，近似線は十分に信頼できる．

A1PからA4Pに変化するに従い，物性α値は2次関数的に大きくなることがわかった．

これまでの知見により，APの物性αの変化とAQのそれは同様の挙動を示すことが示唆されている．

だから，AQシリーズもA1QからA4Qに変化するに伴い，物性αは2次関数的に増加すると考えられる．

そこで，AQのデータに2次回帰曲線（近似線AQ）を引いた．

この近似曲線からA4Qの物性αが最も大きくなり，その値は22 degreeと推論される．

以上の結果より，A4Qを作製し，その物性αを測定することを提案する．

5．まとめ

技術者や科学者はある目的を持って実験します．

実験データがいくつか出てくると，そこから次に進むべき方向を推論しますが，多くの場合は少ないデータでそれを行わねばなりません．

少ないデータから，それの示すことを適切に推論し，推論結果に基づき進むべき方向を，わかりやすく論理的にレポートにまとめて提案できれば，それは上司から好意を持って認められるでしょう．

本稿は，データに基づき推論する方法，およびそれをわかりやすく論理的にレポートにまとめる方法について，述べます．

データの解析法は，一般的に，2つの変数間の関係をグラフ化して，相関性を求めたり，回帰分析を行うことが多いです．

このとき，解析方法は複数あると思うとよいです．

考えられるすべての方法で解析して，その後，より合理的で論理的なものを選びます．
ここ大事です．

本稿では，ある架空の材料Xを取り上げて，その部材の組み合わせと物性αとの関係を求め，その最高値を推論しました．

レポートの書式と書き方は以下のとおりです．

・題名
主題と目的を記します．

・本文
目的を述べます．それは，レポートで報告したいことで，何のために，何をするのか，です．

推論プロセスの概要を述べます．

ここで，データを表や図にまとめて示します．

ついで，データの解析プロセスと結果，およびそれからの推論過程を，論理的でわかりやすい文章で簡潔に記します．

そのレポート例を示しました．