1．はじめに

ある課題について
データや確かなエビデンス（根拠・証拠）を持っていないことが多くあります．
そもそも課題自身についてもよく知らないときもあります．

たとえば「アメリカのシカゴ市には何人のピアノ調律師がいるか？」と問われても，
課題そのものがよくわかりません．

考えるネタが乏しい状況は，
科学技術を始めとして仕事や日常生活の多くの場面で遭遇します．
これらの課題の解を求められると困ります．

ところが，正確ではないが正解に近い解を導く思考法があるのです．
それがフェルミ推定です．

フェルミ推定は，物理学者エンリコ・フェルミが創り出したと言われている思考法で，
課題に関する情報が少ないとき，大胆に推理することにより解を求める方法です．

科学技術者，ビジネスパーソンや学生など多くの人がこの思考法を身に付けておくと，
いろいろな場面で役に立ちます．

それは何か，どのように使うのか，以下に述べます．

2．フェルミ推定とは？

1）エンリコ・フェルミはどんな人？

本論に入る前にエンリコ・フェルミについて紹介します．エンリコ・

フェルミはイタリア出身の物理学者でイタリアとアメリカで活躍し，
原子物理学の分野で顕著な業績を残しています．
多くの人工放射性元素をつくり，
その業績でノーベル物理学賞（1938年）を受賞しています．

物理学ではフェルミの名を冠したものがあり，
素粒子の一つであるフェルミ粒子，フェルミウム（100Fm）という人工放射性元素の名前，
固体の電子準位であるフェルミ準位などに，その名を残しています．

マネージャーとしても優れた能力を発揮し，
原子爆弾を開発したマンハッタン計画のリーダーの一人です．

原爆が広島と長崎に投下されたと聞いて，無言だったと伝えられています．
言葉を失ったのだと理解したいです．
そして，その後の水素爆弾の開発は反対しています．

フェルミはものごとの考え方でも，新しい思考法を生み出しました．
それが今回説明するフェルミ推定です．

2）フェルミ推定とは

フェルミ推定とは，課題に関する少ない情報から出発して，
大胆な推理を含めて思考し結論に到達する推論です．

推論とは一定の論理プロセスで推理・推定を含めて思考することです．

課題に対して持っているデータやエビデンスが乏しいとき，
フェルミ推定を使うと正解に近い解を求めることができます．

フェルミ推定の説明でよく例にあげられるのは，
上で述べた「シカゴ市には何人のピアノ調律師がいるか？」です．
フェルミ自身がこの課題を学生に問うたと伝えられています．

もちろん，学生はその数を知りません．
でも，フェルミ推定で概数を求めることができ，
その答えは意外にも実数に近いのです．

3）フェルミ推定の前提条件

フェルミ推定をうまく行うには2つの前提条件があります．

①課題に関する情報が乏しいことです．
課題に対して多くの情報（データやエビデンス）があれば，
ガッチリと論理的に考えて解を求めることができます．

論理的に考える ―論理ツール①（基本論理語）とは―
論理的に考える ―論理ツール②（言葉を用いた論理プロセス）とは―

そうではなくて，課題に関するデータやエビデンスが少ないときが，
この推定の出番になります．

②推論の出発点となる情報は持っています．
出発点になる情報はあります．
課題を解くための出発点となる情報を持っていないと，そもそも推論が始まりません．

3．フェルミ推定の概要

フェルミ推定は以下のプロセスで推論します．

1）課題を解ける形に変える

課題はそのままでは解けないことがあります．

抽象的な表現やあいまいな表現では，
課題それ自身が何かを議論する羽目になります．
これでは解けません．そのときは，解ける形に変えます．

2）小さな問い（課題を解くための問い）に分解し，それらを順序づける

次に，課題をいくつかの小さな問いに分解します．

課題を解くための最少の情報は何かを考えて，
それを問いの形にします．取っかかりを作り，
かつ解きやすい問いに変えると言ってもよいです．

問いは出発点になる情報からスタートし，
問いに答えていくと課題の解に到達するように順番に並べます．

一般に，解くべき課題は大きすぎてそのままでは解けないことが多いです．
そこで，課題を小さな問いに分けて解きやすい形にします．

これは，データやエビデンスを多く持っているときでも，
いまのようなケースでも当てはまります．

課題を小さな問いに分けることは，課題解決の基本です．

論理的に考える―論理的思考の基本―

課題の分解と順序づけのコツは3つです．

3）問いに答える

問いの答えを求めます．
自分のいま持っている情報のみを使って答えます．

ここがポイントです．
インターネットや本などで調べたい衝動に駆られますが，
それを行わないのがフェルミ推定の大きな特徴です．

なぜでしょうか？
私たちは常に正確な情報を簡単に入手できるとは限りません．
むしろ，情報が不足することがデフォルト（常態）です．

そのようなときにでも，そのようなときだからこそ，
正解に近い解を求める推論がフェルミ推定なのです．

答えを求めるには，自分の持っている知識をフル動員し，
かつヤマカンも大いに使います（いわゆるエイヤーで決めることです）．

これらを存分に使って大胆に推理します．
ここがミソなのです．意外にもこれが当たるのです．

「考える」というと，「論理的に思考する」と認識する人がほとんどでしょう．
もちろん論理的思考は重要です．
それがないと考えることはできません．

さらに，ヤマカンも動員することが大事なのです．
情報が足りないとき，カンで補うことは人が考える常道です．

大事にしてよいです．実はヤマカンも合理的思考と関係しています．
それは第5項で述べます．

4）課題の解を求める

問いに順番に答えていきます．最後に課題の解に到達します．

そのように問いを作っていればこの過程は楽ですし，必ず解が得られます．

5）フェルミ推定の成功条件

フェルミ推定を成功させる条件は以下のとおりです．

①課題に関して少しは知識を持っていること

さすがに取っかかりがまったくないことは解けません．

②論理的思考力を持っていること

課題を解ける形にすることや課題を分解することは，
論理的思考力がないとできません．

問いを解くときも論理的思考力をフル動員しないと解けません．

③ヤマカンを働かせること

ヤマカンはでエイヤーで決めることも必要です．

それが十分な力を発揮することは例題を解いてみるとよくわかるでしょう．

④自分の知識とヤマカンを信じること

自信を持って（自信がなくてもある振りをして）大胆に推理することです．

6）フェルミ推定の効用

フェルミ推定を身に付けると大きな効用があります．

①正解に近い解を，短時間でかつ省エネルギーで獲得することができます
情報入手は多大な時間と労力を要します．
それに対して，フェルミ推定は自分の持っている知識だけの推論ですから，
短時間で省エネ思考です．

②自分の頭で論理的に考える力を鍛錬します
フェルミ推定は自分の頭を頼りにして考えます．
フェルミ推定を使い，プロセスを検証すると，それが鍛えられます．
逆に言えば，自分の頭で論理的に考えられる人はフェルミ推定もうまくできます．

③知識欲が増し関心が外向きになります
フェルミ推定は，多くの情報（一見関係なさそうな情報も）
を持っていると容易に行えます．
フェルミ推定を行うと，自分の頭に多くの情報を入れたいと思い，
外界のいろいろなことに興味が湧いて知識欲が増します．
自然に関心が外向きになります．

4．例題を解いてフェルミ推定を習得する

例題を解いてみるとフェルミ推定の中身を理解できますし，やり方を習得できます．

「シカゴ市には何人のピアノ調律師がいるか？」の解き方は，他に譲ります．

たとえば，「超予測力」（フィリップ・E・テトロック，ダン・ガートナー著，土方奈美訳，早川書房，2016年）という本の
p.151～156に詳しい説明が載っています．
インターネットにもあります．興味のある方はそちらを参照してください．

ここでは以下の課題を解いてみましょう．
次項でその解を実際のデータと照合して，それらの差異を検証します．

課題

日本の2016年における自家用車の販売台数は何台か？
ここで，この課題に関して，日本の人口は約1億3000万人という情報を持っているとし，
この情報からフェルミ推定をスタートするとします．

1）課題を解ける形に変える

課題が解きにくい場合や抽象的な場合には，
課題を解きやすい形に変えます．

上の課題はどのように解いていったらよいのか，
取っかかりが見えにくいです．

なので，
「日本の2016年における自家用車の販売数は，
すべて現在所有している自家用車の買い換えによる」
の形に置き換えます．

また，自家用車を乗用車の普通車と小型車の合計台数とします．
こうすると，課題を解くための小さな問いが作りやすくなります．

クレームが出るもしれません．
新規購入者が入らないではないか，と．

確かにそうですが，一定の年齢になると自動車を購入しないと仮定します．
その人数＝新規購入者，とすると上の設定でも問題ありません.
（それが妥当か否かはともかくとして）
　

2）課題を小さな問いに分解し，それらを順序づける

課題に関して知っている情報は，日本の人口（約1億3000万人）だけです．
ここから出発できるように，小さな問いを作ります．

課題を以下の6問に分解して，順番に並べました．

　
問いは以下のように作りました．
その図解を図1に示します．

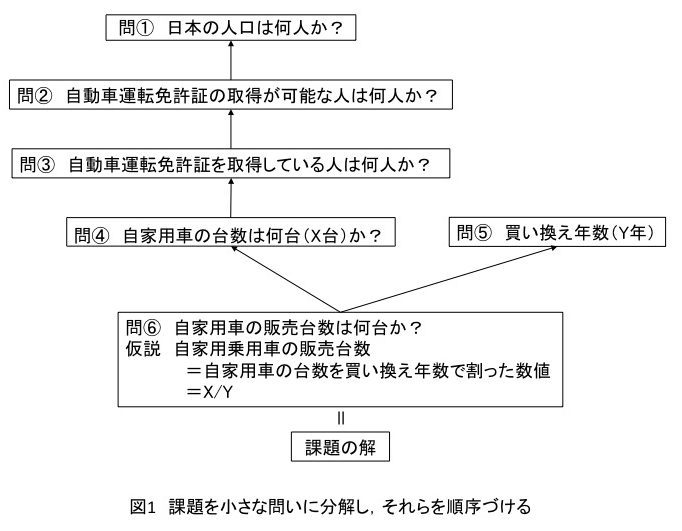
課題を，自家用車の販売数は，すべて自家用車の買い換えによる，としました．

自家用車は一定の年数所有した後すべて買い換える，との仮説をつくって，
それが正しいとして解くことにしたのです．
つまり，自家用車の販売数＝自家用車の買い換え台数，です．

これは，自家用車の台数をX台とし，買い換えの年数（何年所有したら買い換えるか）をY年とすると，
X/Y＝自家用乗用車の販売台数，とすることです．

なお，「自家用車の台数」とは，
人（厳密に言えば2016年の日本国内にいる人）に所有されている自家用車の台数です．

販売店やメーカーにある自動車は除きます．
自家用車とは乗用車の普通車と小型車であり，
ここでの議論は1年（2016年）の販売台数です．

そうなると，自家用車の台数（X台）と買い換えの年数（Y年）が知りたい情報です．
自家用車の台数は，自動車運転免許証を持っている人数から推理できそうです．

そこで，自動車運転免許証を持っている人数を求めます．
それは日本の人口から，運転免許証の取得が可能な人数を推理し，
そこからさらに推理を続ければ求められそうです．

日本の人口は知っている情報（出発点）ですから，
ここをスタート点として，上の事項を問いの形にして順番に並べました．

このように，問いは，必要なら課題を解ける形にして，
そこから出発点に遡(さかのぼ)るように論理的な筋道を考えます．

それらを問いの形にして出発点から並べると，課題を解くための問いができあがります．

3）問いに答えて，課題の解を求める

筆者の答え（推定値）を表1にまとめました．

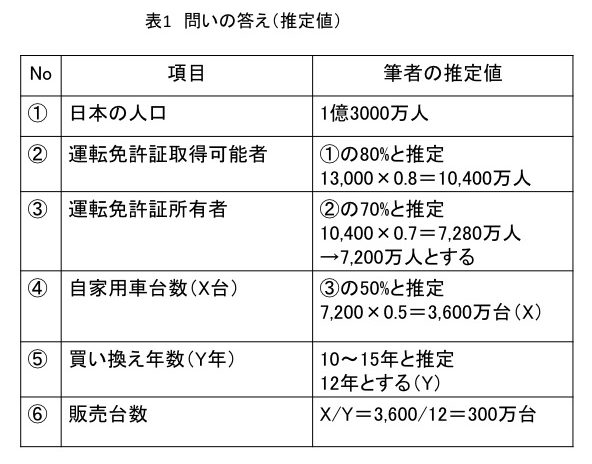
①日本の人口は何人か？
日本の人口は約1億3000万人です．これは知っていました．
2016年も同じとして，答えを1億3000万人としました．

②自動車運転免許証の取得が可能な人は何人か？
これは情報を持っていません．なので推理します．

運転免許証は18歳から取れますから，
この問いは18歳以上の人が何人か，と同じです．

日本の人口は0歳から90歳までとします．
90歳以上の人は数が少なくなりますので，ここではゼロとしました．

各年齢の人数を同数とします．
厳密には各年齢の人数は異なりますが，ここでは同数としておきます．

そうすると18歳以上は人口の80%になります．
13,000万人×0.8＝10,400万人ですから，
この問いの答えを1億400万人と推定しました．
　
③そのうち自動車運転免許証を持っている人は何人か？
これもわかりません．
地方では自動車が必需品と聞いていますが，
都市部ではそうでもないし，若者にクルマ離れがあると聞いています．

そこで，推理します．
地方と都市部の人口は同一とします．

地方では該当者はすべて運転免許証を持っている（100%）とし，
都市部では半分もいない（40%ぐらいか）とします．

そうすると，免許証所得可能者のうち70%が免許証を持っていると推定できます
（数式で示すと，100%×1/2＋40%×1/2＝70%，です）．

運転免許証を持っている人は，
10,400万人×0.7＝7,280万人，です．
7,200万人と概数にして以下に使います．

④自家用車の台数は何台か（X台）？
わかりません．
運転免許証を持っている人はすべて自家用車を持っているとは限りません．
ペーパードライバーもいます．

また，家族で1台の自家用車を持っていたり，
1人で複数の自家用車を持っている人もいるようです．
でも後者は少ないと思います．

そこで，ヤマカンで運転免許証を持っている人の50%が自家用車を持っているとし，
その数値を自家用車の台数とします．

自家用車の台数（X台）は
7,200×0.5＝3,600万台です．

⑤自家用車は何年ごとに買い換えられるのか（Y年＝買い換え年数）？
わかりません．
自家用車は10～15年で買い換えると聞いたことを思い出しました．
なので，ここではヤマカンで12年（Y年）とします．

⑥自家用車の販売台数は何台か？
問いを作ったとき，自家用車の販売台数＝X/Y，としましたので，それを使います．
X/Y＝3,600/12＝300万台

⑦課題の解を求める
⑥の答え300万台が課題の解です．

4）解の検証

課題の解と問いの正しい答えは，統計データにありますので検証します．

表2に問いの答え（筆者の推定値）と統計データとの比較を示します．

①日本の人口は何人か？
日本の人口は総務省統計局の人口推計によると，
2016.12.20.現在で1億2710万人です．

約1億3000万人との知識はほぼ正しかったです．

②自動車運転免許証の取得が可能な人は何人か？
総務省統計局の人口推計には20～89歳の人口データがあります．

18歳から19歳は16歳～19歳の中に入っていますので，
これは使わないで20歳以上のデータを使いました．

18～19歳が入らないのですがやむを得ません．
2016.12.20.現在で1億331万人です．

1億400万人と推定しましたが，かなり近い数値です．
各年齢の人数を同一としたのは概算としては間違っていないのです．

③そのうち自動車運転免許証を持っている人は何人か？
自動車運転免許証の所得者数は，警察庁運転免許統計からわかります．
2016年度のデータによると8,221万人です．

推定値7,280万人とは約1000万人離れています．
推定値なのでこのくらい乖離(かいり)することがあります．

推定値を70%から80%に変更すると8,320万人になりますから，
統計データに近い値となります．

都市部で免許証を持っている人の割合を，
推定値「半分もいないー40%ぐらいか」より高くして「半分以上（60%ぐらいか）」とすると，
上の数値になります．真実はこれに近いのでしょう．

④自家用車の台数は何台（X台）か？
自家用車台数は，自動車検査登録情報協会にデータがあります．
2016.3月現在の乗用車（普通車と小型車）は3,912万台です．
推定値3,600万台は近い値です．

運転免許証所有者数は正確な数値と乖離(かいり)していました．
推定では自家用車台数を運転免許証所有者の50%と推理したのですが，
結果的には近い数値が得られました．

ヤマカンの50%が結果的にはOKだったのです．
正しくは運転免許証所有者の48%になります．
50%という推理は真実に近いです．ヤマカンも有効です．

また，フェルミ推定ではいくつかの推理を重ねると
（ここでは2つ）意外に真実に近い値になることがあります．

⑤自家用車は何年ごとに買い換えられるのか（Y年＝買い換え年数）？
このデータは見つかりませんでしたので，この判定はできません．

⑥自家用車の販売台数は何台か？
自動車の販売台数は，日本自動車販売協会連合会にデータがあります．
2016年の乗用車（普通車と小型車）の販売台数は280万台です．
推定値300万台は近い値です．

今回のフェルミ推定は運転免許証所有者数が
真実値8,221万人に対して推定値7,200万人と約1000万人離れましたが，
それ以外は推定値と真実値は近い値になりました．

このように，フェルミ推定では出発点の情報から始めて，
論理的やヤマカンで推理することにより，正解に近い解を求めることができます．

上の例のようにある段階ではヤマカンでエイヤーと決めますが，
人の思考は論理的でもヤマカンでも正しい方向へ進みます．

それは問いの内容と順序が論理的・合理的だからです．

推定値がある程度離れていてもいくつかのステップを経ると正しい方向へ修正されます．
フェルミ推定は，情報が少ない状況下で課題の解を求めるときに有効なのです．

5．練習問題

練習問題を解いてみましょう．

以下の課題を，フェルミ推定を使って解いてください．

ここで，東京都の人口を1,400万人（2016年）として，
このデータを出発点として推定を始めてください．

解答例と検証はこちらです．
→フェルミ推定 その2 【フェルミ推定の事例】

6．まとめ

1）ある課題についてデータや確かなエビデンス（根拠・証拠）を持っていないことが多くあります．そもそも課題自身についてもよく知らないときもあります．そのようなとき，正確ではないが正解に近い解を導く思考法があります．それがフェルミ推定です．

2）フェルミ推定は，物理学者エンリコ・フェルミが創り出したと言われている思考法で，課題に関する情報が少ないとき，大胆に推理することにより解を求める方法です．
科学技術者，ビジネスパーソンや学生など多くの人がこの思考法を身に付けておくと，いろいろな場面で役に立ちます．

3）フェルミ推定の概要は以下のとおりです．
①課題を解ける形に変える
②小さな問い（課題を解くための問い）に分解し，それらを順序づける
③問いに答える
④課題の解を求める

4）フェルミ推定の成功条件
フェルミ推定を成功させる条件は以下のとおりです．
①課題に関して少しは知識を持っていること
②論理的思考力を持っていること
③ヤマカンを働かせること
④自分の知識とヤマカンを信じること

5）フェルミ推定の効用
　フェルミ推定を身に付けると大きな効用があります．
①正解に近い解を，短時間でかつ省エネルギーで獲得することができます
②自分の頭で論理的に考える力を鍛錬します
③知識欲が増し関心が外向きになります

6）例題を解き，その解を検証しました．検証した結果，フェルミ推定で得られた解は真実値に近い値だとわかりました．